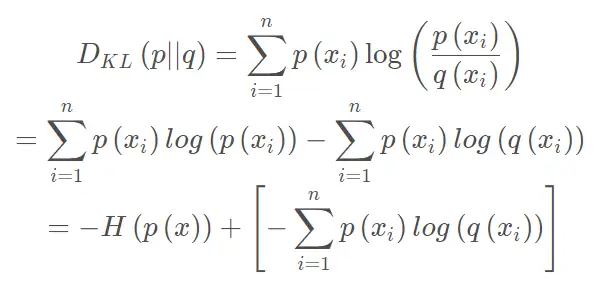Kullback-Leibler Divergence
Kullback-Leibler Divergence
Kullback-Leibler Divergence
Kullback-Leibler散度（通常缩短为KL散度）是一种比较两种概率分布的方法。在概率论和统计学中，我们经常用更简单的近似分布来代替观察到的数据或复杂的分布。KL散度帮助我们衡量在选择近似值时损失了多少信息。
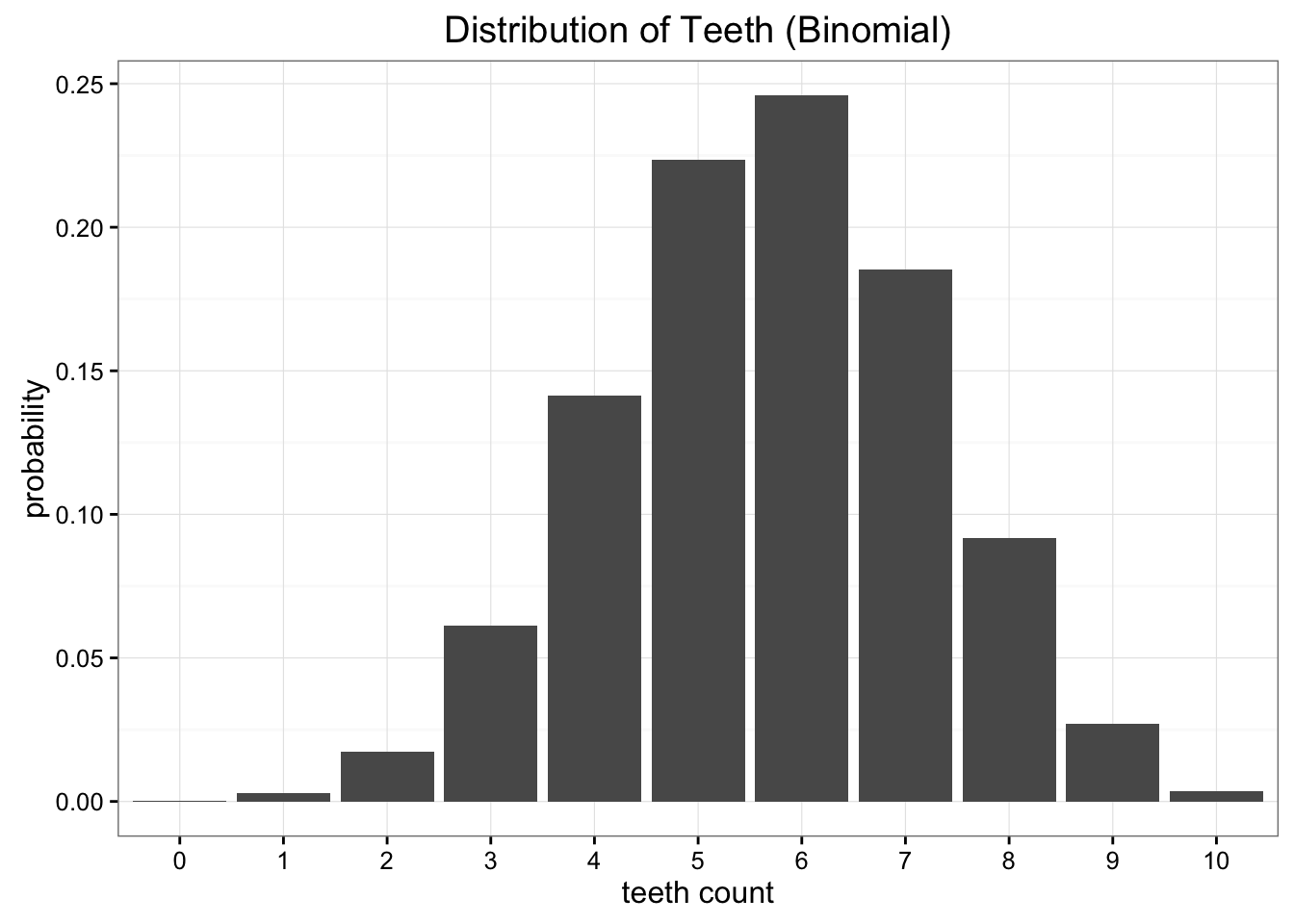
假设发现一种蠕虫,牙齿一原本共十颗,但有些有缺失,牙齿分布如下:
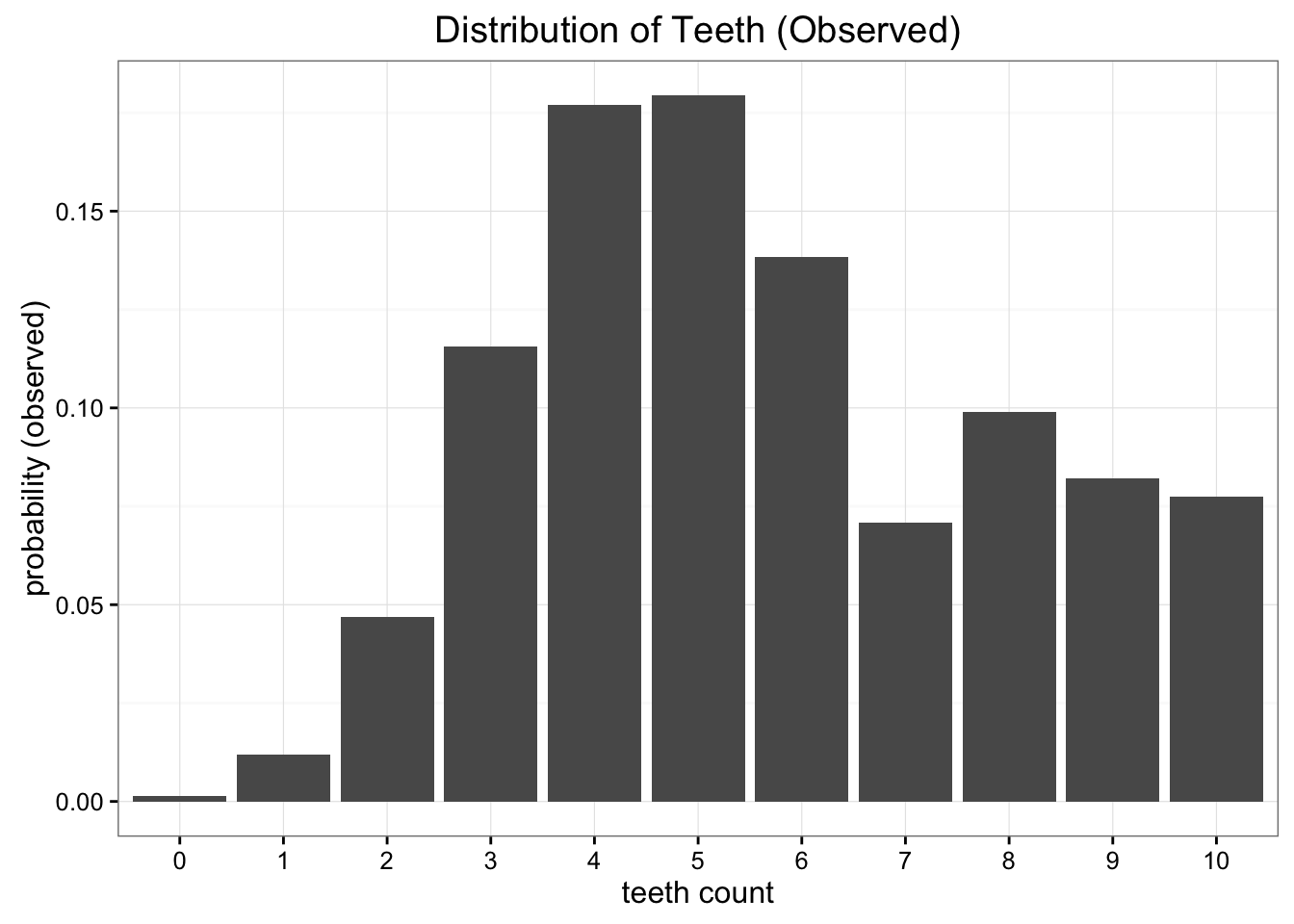
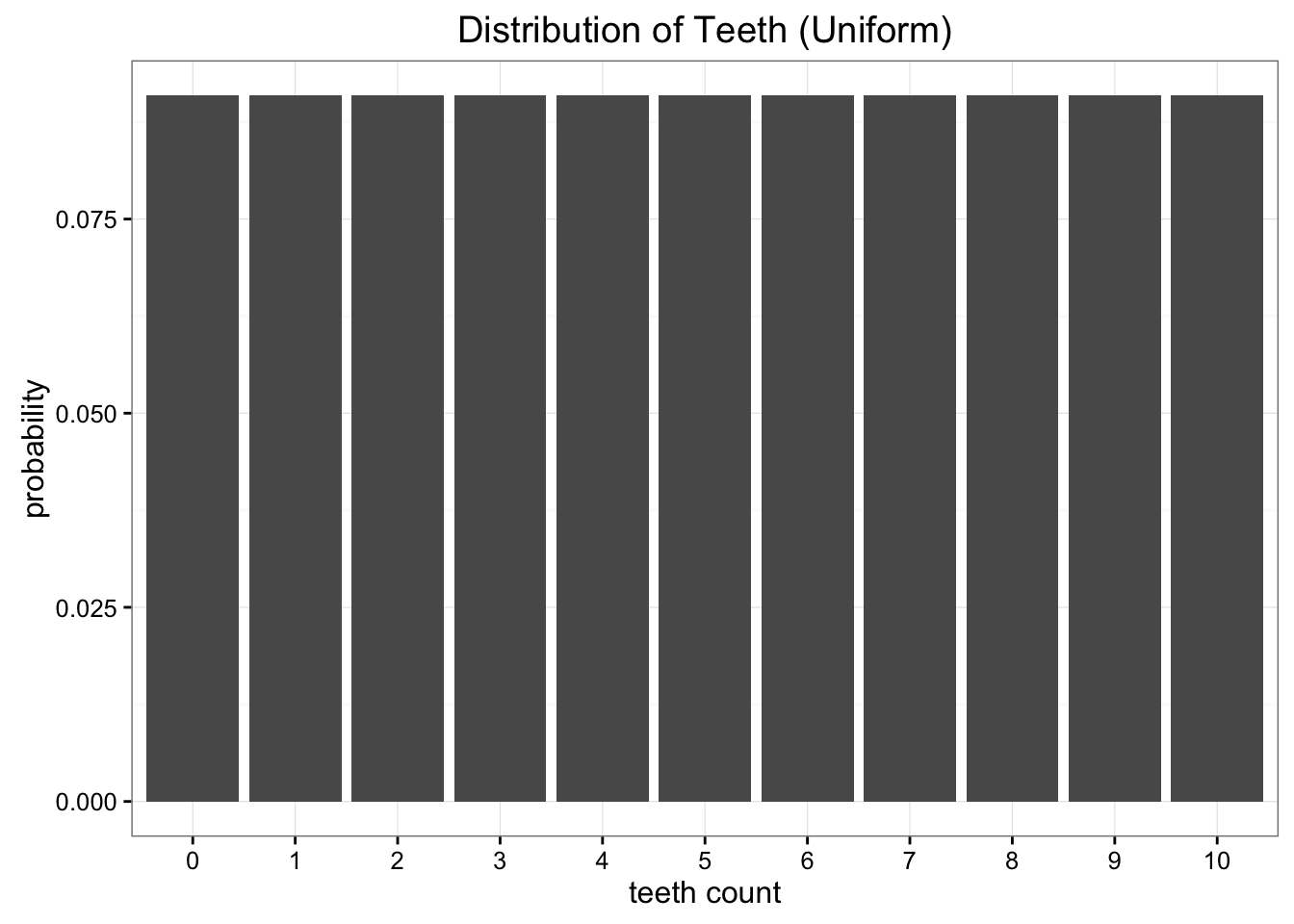
我们想做的是将这些数据简化为一个只有一两个参数的简单模型。一种选择是将蠕虫牙齿的分布表示为均匀分布,明显这种表示有一点问题.
如果使用二项分布,需要n和p两个参数.
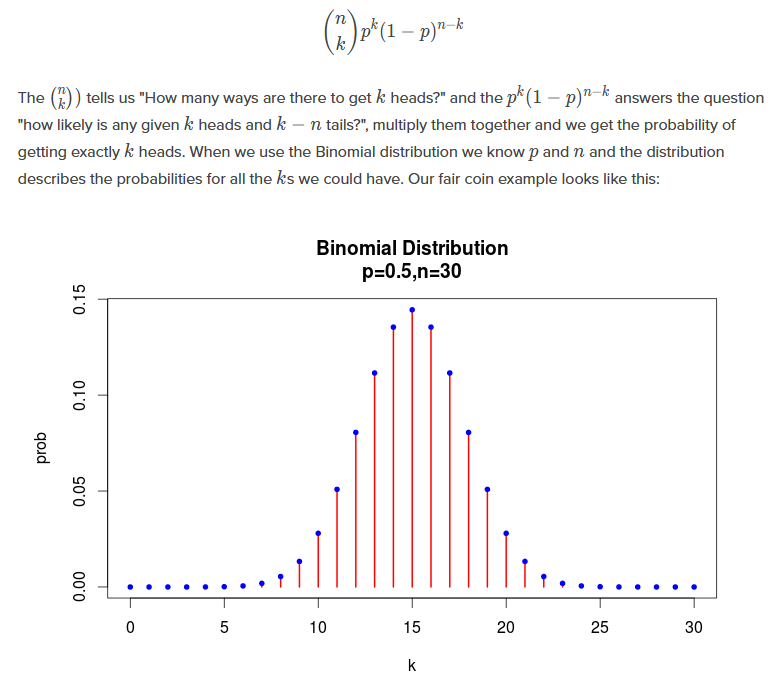
原始数据平均值若为5.7,则p=0.57最好,此时E[x]=n*p=5.7
然后需要比较这两种模型代替原始数据谁更好.
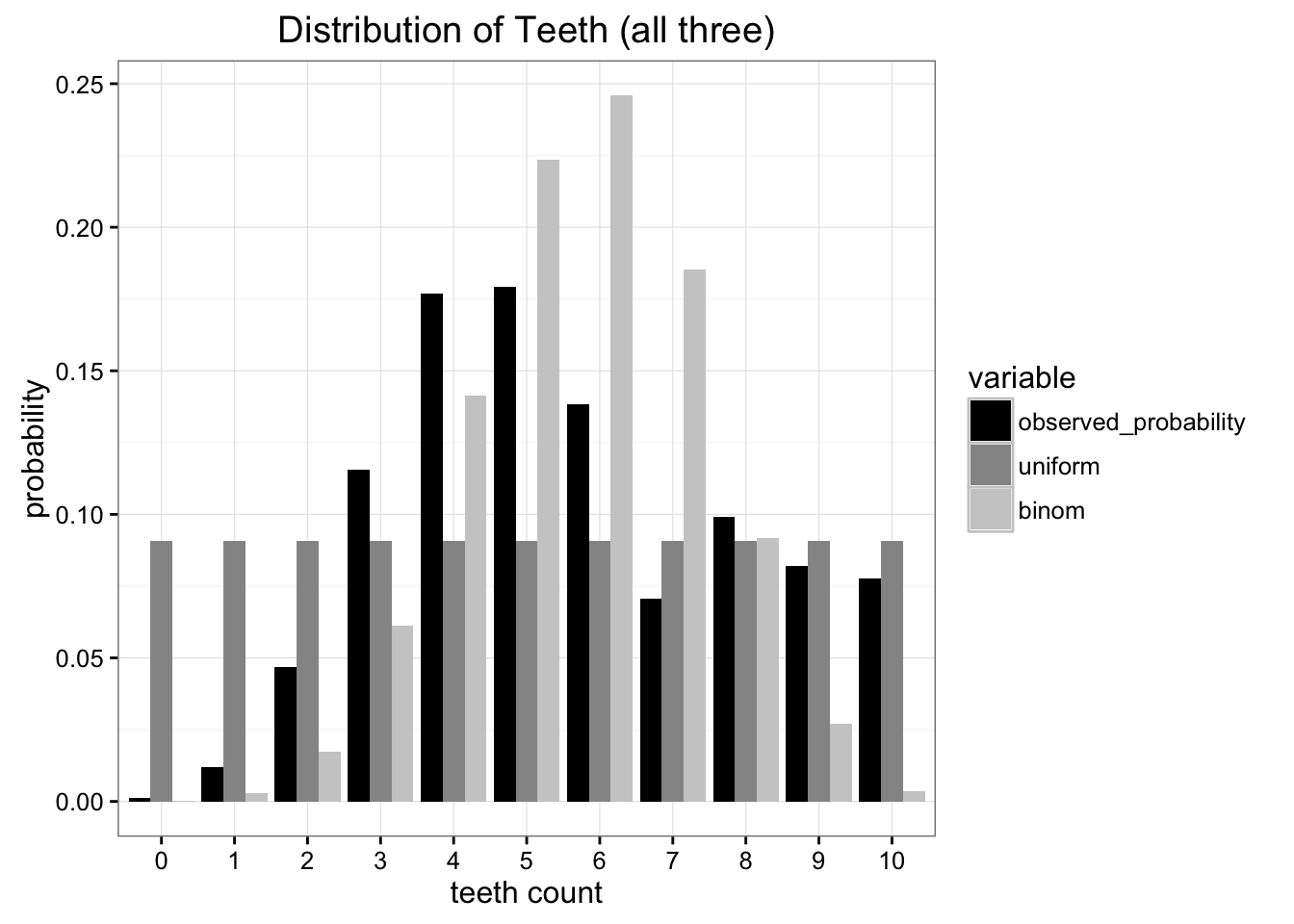
现有的度量方式有很多，但我们主要关心的是尽量减少必须发送的信息量。这两个模型都将我们的问题简化为两个参数，牙齿数和概率（尽管我们实际上只需要均匀分布的齿数）。
最好的测试是哪个分布保存了来自原始数据源的最多信息。这就是Kullback Leibler Divergence的用武之地。
这时候需要引入熵的概念, $$ H=-\sum_{i=1}^Np(x_i)\cdot\log p(x_i) $$ KL起源于信息论。信息论的主要目标是量化数据中的信息量。
熵没有告诉我们的是帮助我们实现这种压缩的最佳编码方案。信息的最佳编码是一个非常有趣的话题，但对于理解KL分歧来说并不是必要的。
熵的关键在于，只要知道我们需要的比特数的理论下限，我们就可以准确地量化数据中的信息量。
Kullback-Leibler散度只是对我们的熵公式的一个轻微修改。 $$ D_{KL}(p||q)=\sum_{i=1}^Np(x_i)\cdot(\log p(x_i)-\log q(x_i)) $$ 本质上，我们所看到的KL散度是原始分布中数据的概率与近似分布之间的对数差的期望。
利用KL散度，我们可以准确地计算出当我们用另一个分布近似一个分布时损失了多少信息 $$ D_{kl}(\text{Observed}\mid\mid\text{Uniform})=0.338 \ D_{kl}(\text{Observed}\mid\mid\text{Binomial})=0.477 $$ 将KL散度视为距离度量可能很诱人，但我们不能使用KL散度来测量两个分布之间的距离。这是因为KL散度不是对称的。
我们可以尝试依旧使用二项分布,但改变参数p对KL进行优化
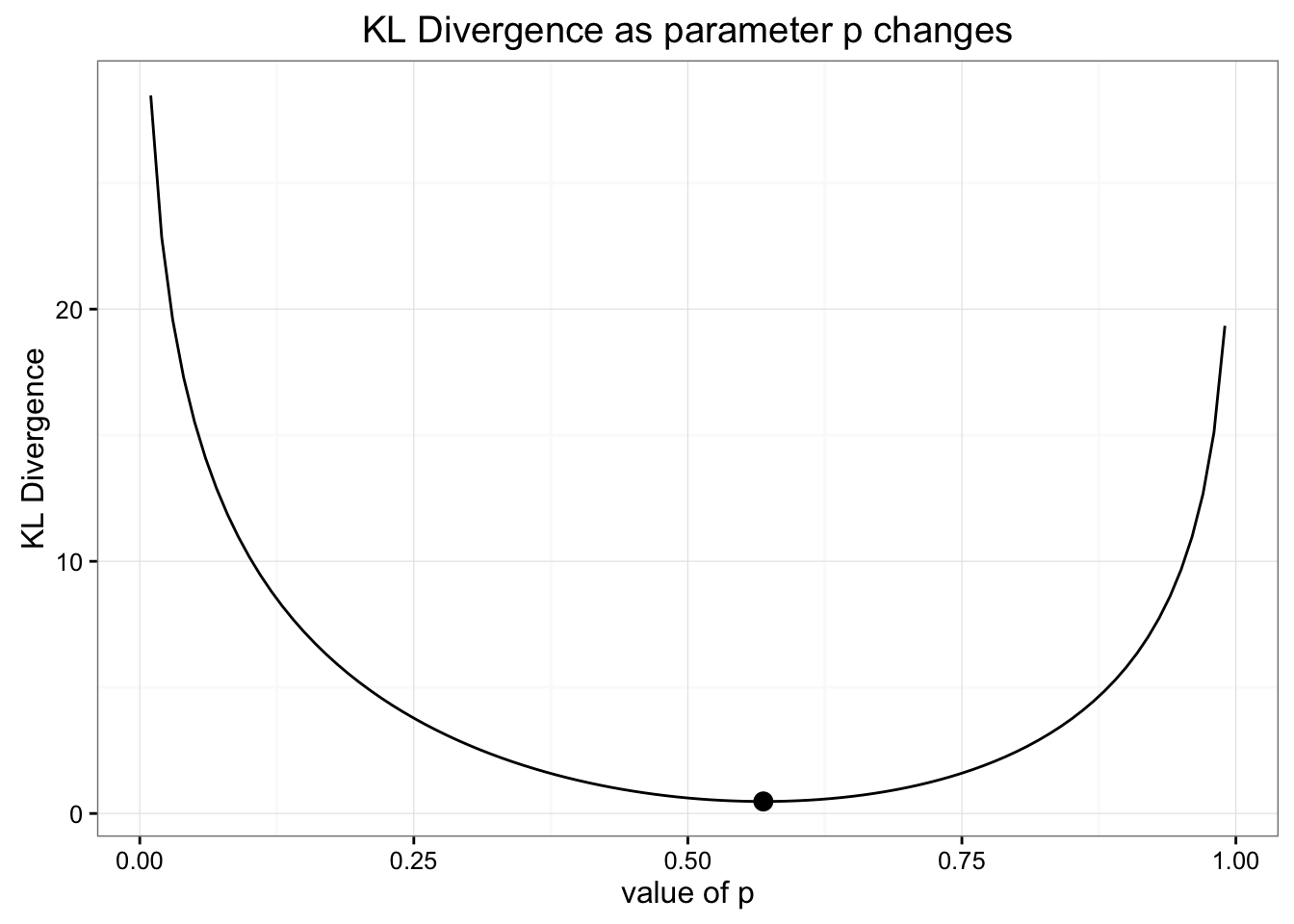
结果发现p正是在n*p=E(original_data)时,KL最优.
如果自己定义一个模型,假设0-5的牙齿数概率相等且和为p,则6-10概率为1-p
有
$$
[6,11]=\frac p5;[0,5]=\frac{1-p}6
$$
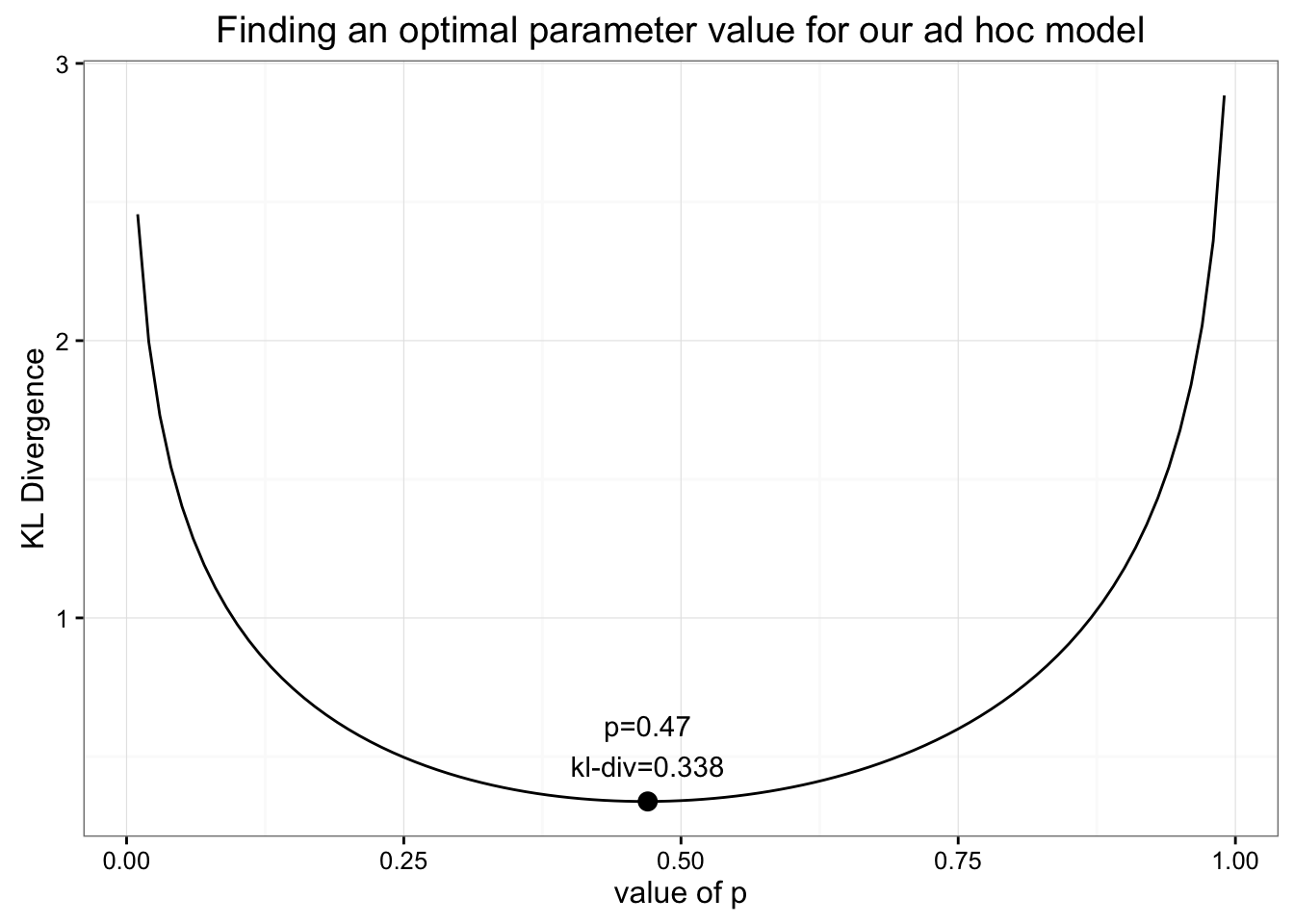
最优值p=0.47,发现此时KL与之前均值分布时相等.
KL与信息熵和交叉熵的关系如下
